Kolmogorov Smirnov Test

One sample Kolmogorov–Smirnov test of the null hypothesis that data in the sample is a random sample from specified distribution, against the alternative that the distribution is different.

This topic contains the following sections:

Kolmogorov-Smirnov Test Specification
Implementation
Code Sample
See Also

Kolmogorov-Smirnov Test Specification

The empirical distribution function F_n for n independent and identically distributed observations X_i is defined as

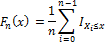
where 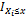HT Ix is the indicator function, equal to 1 if X_i ≤ x and equal to 0 otherwise.

The Kolmogorov–Smirnov statistic for a given cumulative distribution function F(x) is:

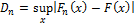
where sup_x is the supremum of the set of distances. If the sample comes from distribution F(x), then D_n converges to 0 almost surely. In practice, the statistic requires a relatively large number of data points to properly reject the null hypothesis.

The null hypothesis is rejected at level α if

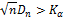
where K_α is found from

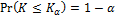
K is the random variable which has Kolmogorov distribution.

Implementation

The following constructors create an instance of KolmogorovSmirnovTest class.

Constructor	Description	Performance
two-tailed test, default significance level	Constructor without parameters. Creates KolmogorovSmirnovTest instance with default significance level for two-tailed test. KolmogorovSmirnovTest
default significance level	Creates KolmogorovSmirnovTest instance with default significance level and user defined tail. KolmogorovSmirnovTest(Tail)
two-tailed test, user defined significance level	Creates KolmogorovSmirnovTest instance for two-tailed test and user-defined significance level. KolmogorovSmirnovTest(Double)
user defined tail and significance level	Creates KolmogorovSmirnovTest instance with user defined significance level and tail. KolmogorovSmirnovTest(Double, Tail)

The class provides the following methods:

Method	Description	Performance
update	Updates test statistic using provided sample and supposition about distribution. Double array series: Update(Double, CUDistribution) Vector series: Update(Vector, CUDistribution)

Method

Description

Performance

update

Updates test statistic using provided sample and supposition about distribution.

Double array series:

method Update(Double, CUDistribution)

Vector series:

method Update(Vector, CUDistribution)

The class provides the following properties:

Property	Description	Performance
region of acceptance	We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance. Region of acceptance left border: AcceptanceRegionLeft Region of acceptance right border: AcceptanceRegionRight
p-value	The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. PValue

Property

Description

Performance

region of acceptance

We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance.

Region of acceptance left border:

Property AcceptanceRegionLeft

Region of acceptance right border:

Property AcceptanceRegionRight

p-value

The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true.

Property PValue

Code Sample

The example of KolmogorovSmirnovTest class usage:

Copy

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class KolmogorovSmirnovTestSample
 9    {
10        static void Main()
11        {
12            //Create an instance of normal distribution.
13            Normal distr = new Normal(0, 1);
14
15            // Generate random series.
16            Vector series = Vector.Random(100);
17
18            // Create an instance of KolmogorovSmirnovTest.
19            KolmogorovSmirnovTest test = new KolmogorovSmirnovTest(0.05, Tail.Both);
20            test.Update(series, distr);
21
22            Console.WriteLine("Test Result:");
23            // Test decision
24            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
25            // The statistic of KolmogorovSmirnovTest test.
26            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
27            // The p-value of the test statistic.
28            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
29
30        }
31    }
32}

Reference

FinMath.Statistics.HypothesisTesting