Kolmogorov Smirnov Two Sample Test

Two sample Kolmogorov–Smirnov test of the null hypothesis that data in the samples are random samples from equal distributions, against the alternative that the distributions are different.

This topic contains the following sections:

Kolmogorov-Smirnov Two Sample Test Specification
Implementation
Code Sample
See Also

Kolmogorov-Smirnov Two Sample Test Specification

The Kolmogorov–Smirnov test may also be used to test whether two underlying one-dimensional probability distributions differ. In this case, the Kolmogorov–Smirnov statistic is

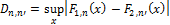
where F_1,n and F_2,n' are the empirical distribution functions of the first and the second sample respectively.

The null hypothesis is rejected at level α if

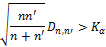
where K_α is found from

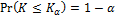
K is the random variable which has Kolmogorov distribution.

Note that the two-sample test checks whether the two data samples come from the same distribution. This does not specify what that common distribution is (e.g. normal or not normal).

Implementation

The following constructors create an instance of KolmogorovSmirnovTest class.

Constructor	Description	Performance
two-tailed test, default significance level	Constructor without parameters. Creates KolmogorovSmirnovTwoSampleTest instance with default significance level for two-tailed test. KolmogorovSmirnovTwoSampleTest
default significance level	Creates KolmogorovSmirnovTwoSampleTest instance with default significance level and user defined tail. KolmogorovSmirnovTwoSampleTest(Tail)
two-tailed test, user defined significance level	Creates KolmogorovSmirnovTwoSampleTest instance for two-tailed test and user-defined significance level. KolmogorovSmirnovTwoSampleTest(Double)
user defined tail and significance level	Creates KolmogorovSmirnovTwoSampleTest instance with user defined significance level and tail. KolmogorovSmirnovTwoSampleTest(Double, Tail)

The class provides the following methods:

Method	Description	Performance
update	Updates test statistic using provided samples. User specifies two double array samples and offsets and number of elements to use in each sample: Update(Double, Int32, Int32, Double, Int32, Int32)

Method

Description

Performance

update

Updates test statistic using provided samples.

User specifies two double array samples and offsets and number of elements to use in each sample:

method Update(Double, Int32, Int32, Double, Int32, Int32)

The class provides the following properties:

Property	Description	Performance
region of acceptance	We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance. Region of acceptance left border: AcceptanceRegionLeft Region of acceptance right border: AcceptanceRegionRight
p-value	The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. PValue

Property

Description

Performance

region of acceptance

We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance.

Region of acceptance left border:

Property AcceptanceRegionLeft

Region of acceptance right border:

Property AcceptanceRegionRight

p-value

The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true.

Property PValue

Code Sample

The example of KolmogorovSmirnovTest class usage:

Copy

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class KolmogorovSmirnovTwoSampleTestSample
 9    {
10        static void Main()
11        {
12            //Create instances of normal distribution.            
13            Normal distr1 = new Normal(0, 5);
14            Normal distr2 = new Normal(3, 5);
15
16            // Generate random series.
17            Vector series1 = Vector.Random(100, distr1);
18            Vector series2 = Vector.Random(150, distr2);
19
20            // Create an instance of KolmogorovSmirnovTwoSampleTest
21            KolmogorovSmirnovTwoSampleTest test = new KolmogorovSmirnovTwoSampleTest(0.05, Tail.Both);
22            test.Update(series1, series2);
23
24            Console.WriteLine("Test Result:");
25            // Test decision
26            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
27            // The statistic of KolmogorovSmirnovTwoSampleTest test.
28            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
29            // The p-value of the test statistic.
30            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
31
32        }
33    }
34}

Reference

FinMath.Statistics.HypothesisTesting