Pearsons ChiSquared Test |
One sample Pearson’s χ2 test of the null hypothesis that frequency distribution of events in the sample is consistent with provided theoretical distribution.
This topic contains the following sections:
A test of goodness of fit establishes whether or not an observed frequency distribution differs from a theoretical distribution.
The algorithm is the following:
Calculate the chi-squared test statistic, χ2, which resembles a normalized sum of squared deviations between observed and theoretical frequencies (see below).
Determine the degrees of freedom, d, of that statistic, which is essentially the number of frequencies reduced by the number of parameters of the fitted distribution.
Compare χ2 to the critical value of no significance from the χ2-distribution.
When testing whether observations are random variables whose distribution belongs to a given family of distributions, the "theoretical frequencies" are calculated using a distribution from that family fitted in some standard way.
We can do the formalization as follows. Fix n bins:
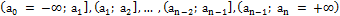
covering the whole of (-∞;+∞), where ai are bin edges.
Hitting probabilities pi are the probabilities of hitting bins from left to right in supposed distribution.
Test statistic is calculated as follows:
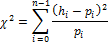
where hi are hits frequency, i.e. the frequency of observations in the particular bin i.
The chi-squared statistic can then be used to calculate a p-value by comparing the value of the statistic to a chi-squared distribution.
The degrees of freedom are calculated as d= n-s-1, where s is the number of parameters used in fitting the distribution.
The following constructors create an instance of PearsonsChiSquaredTest class.
Constructor | Description | Performance |
|---|---|---|
default significance level | Constructor without parameters. Creates PearsonsChiSquaredTest instance with default significance level. | |
user defined significance level | Creates PearsonsChiSquaredTest instance with user defined significance level. |
The class provides the following update methods:
Method | Description | Performance |
|---|---|---|
set bin edges and hitting probabilities | Updates test statistic using provided sample. Edges of bins should be sorted in acceding order and should NOT include left edge of the leftmost bin and right edge of the rightmost bin (–∞ and +∞ will be assumed as this two edges correspondingly). Hitting probabilities must be sorted from left to right and must have same size as binEdges vector. Each element should be in [0, 1]. hittingProbabilities[0] is probability of hitting bin (–∞, binEdges[0]]. hittingProbabilities[i] for i > 0 is probability of hitting bin (binEdges[i-1], binEdges[i]]. Probability of hitting rightmost bin is computed as 1 – (sum of all elements of hittingProbabilities). Double array sample:
Vector sample: | |
set distribution, 10 bins by default | Updates test statistic using provided sample. Edges of bins will be chosen to make all bins equiprobable for hitting by supposed distribution sample. Double array sample:
Vector sample: | |
set bins number and distribution | Updates test statistic using provided sample. Edges of bins will be chosen to make all bins equiprobable for hitting by supposed distribution sample. Double array sample:
Vector sample: | |
set bin edges and distribution | Updates test statistic using provided sample. Edges of bins should be sorted in acceding order and should NOT include left edge of the leftmost bin and right edge of the rightmost bin (–∞ and +∞ will be assumed as this two edges correspondingly). Double array sample:
Vector sample: |
The class provides the following properties:
Property | Description | Performance |
|---|---|---|
region of acceptance | We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance. Region of acceptance left border: Region of acceptance right border: | |
p-value | The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. |
The example of PearsonsChiSquaredTest class usage:
1using System; 2using FinMath.LinearAlgebra; 3using FinMath.Statistics.HypothesisTesting; 4using FinMath.Statistics.Distributions; 5 6namespace FinMath.Samples 7{ 8 class PearsonsChiSquaredTestSample 9 { 10 static void Main() 11 { 12 // Create an instance of normal distribution. 13 Normal distr = new Normal(0, 1); 14 15 // Generate random series. 16 Vector series = Vector.Random(100); 17 18 // Create an instance of PearsonsChiSquaredTest. 19 PearsonsChiSquaredTest test = new PearsonsChiSquaredTest(0.05); 20 test.Update(series, distr, 0); 21 22 Console.WriteLine("Test Result:"); 23 // Test decision 24 Console.WriteLine($" The null hypothesis failed to be rejected: {test.Decision}"); 25 // The statistic of PearsonsChiSquaredTest. 26 Console.WriteLine($" Statistics = {test.Statistics:0.000}"); 27 // The p-value of the test statistic. 28 Console.WriteLine($" P-Value = {test.PValue:0.000}"); 29 30 } 31 } 32}

