Entropy Based Test

For one sample Entropy-Based test we consider the time series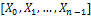

• Tail.Both. In the alternative hypothesis data are not independent or not identically distributed.

• Tail.Left. In the alternative hypothesis values tend to have too long increasing/decreasing sequences.

• Tail.Right. In the alternative hypothesis values tend to alternate increases and decreases.

Note
Decision based on P-value and significance level comparison is more exact.

We look at the difference between two consecutive numbers: X₁ - X₀, X₂ - X₁, ..., X_n-2 - X_n-1. Ignoring the zero differences, we record the sequence difference using plus signs for X_i - X_i-1 > 0, and minus signs otherwise.

Naturally, for a random process, we expect that there are roughly equal numbers of both signs. By the central limit theorem, the number of positive signs P converges weakly to N(m/2; m/4) if there are m non-zero values of X_i - X_i-1. This simple fact can also serve as a test for randomness.

However, this test certainly can not reject the case such as half positive signs followed by half negative signs. The cluster of positive signs means that an up trend happens in the sequence; The cluster of negative signs corresponds to a down trend. Lasting up or down trends certainly should not appear in a random sequence. So, again we look at the number of runs of consecutive positive or negative differences: r. A run up starts with a plus sign and a run down starts with a minus sign.

The exact distribution of r under the null hypothesis of randomness can be obtained by calculating all possible permutations and combinations. When the number of observations is large, say n > 128, the asymptotic distribution of r is r ~ N(μ₂, σ₂²), where

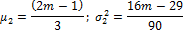
The test statistic is calculated as:

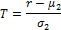
When we estimate H(P) from a given sequence, the direct way is to get the approximate probability distribution:

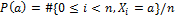
We can obtain estimation for entropy by looking at the approximate probability distribution P^(r)(n) of overlapping r-tuples of down/up runs. Estimation of entropy can be obtained as:

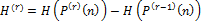
Under the null hypothesis, the probability of getting the exact number of runs for a two-tailed test, not less (not greater) number of runs for a left- (right-) tailed test is calculated.

The following constructors create an instance of EntropyBasedTest class.

The class inherits the update methods from its parent OneSampleTest class.

The class provides the following properties:

The example of EntropyBasedTest class usage:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4
 5namespace FinMath.Samples
 6{
 7    class EntropyBasedTestSample
 8    {
 9        static void Main()
10        {
11            // Generate random series.
12            Vector series = Vector.Random(100);
13
14            // Create an instance of EntropyBasedTest.
15            EntropyBasedTest test = new EntropyBasedTest(0.05, Tail.Both);
16            test.Update(series);
17
18            Console.WriteLine("Test Result:");
19            // Test decision
20            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
21            // The statistic of EntropyBasedTestTest test.
22            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
23            // The p-value of the test statistic.
24            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
25
26        }
27    }
28}

Reference