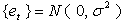Base Terms and Concepts

Given a sample statistic's value, the Null Hypothesis H₀ proposes that the observed test value is merely due to chance but not due to a systematic cause. The null hypothesis is opposite to what the researcher expects; researcher's expectancy of a systematic cause is referred to as the Alternative Hypothesis H₁.

The null hypothesis is examined to either accept or reject, strong interpretation of test result is as follows:

• Rejecting of the null hypothesis directly means that the given estimation is unfit for practical use for lack of statistical significance;

• Accepting of the null hypothesis means that we failed to reject H₀.

Technically, Hypothesis Testing works by measuring of how probable the observed statistic's value is; for this, the p-value is calculated which is the probability of observing data at least as extreme as that is observed, assuming that the null hypothesis is true. If the obtained p-value exceeds some predefined threshold then the observation is consistent with the null hypothesis, otherwise the observed value is considered as very improbable and the researcher concludes that the null hypothesis is false (rejected).

As every statistical decision, the conclusion can be fallacious because of the inevitable noise in the data and/or poor sampling.

The diagram below illustrates schematically how errors can occur while null hypothesis testing. A given set of known population samples can be divided into the two subsets so that one subset results in the true null hypothesis H₀ and another leads to the true alternative hypothesis H₁ (black bounds on the diagram). Data noise and/or using of new poor ("unrepresentative") samples make H₀-related subset different from the true one (the red bound on the diagram) what leads to conclusion errors of two types depending on which hypothesis has incorrectly been identified as the true state of nature.

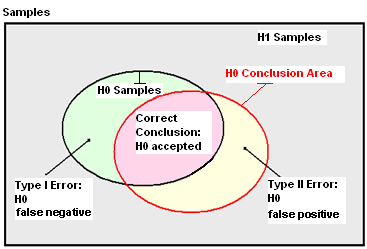
The Type I Error (the green area on the diagram) is the decision to reject the true null hypothesis and is also known as a false positive (positiveness is meant here with respect to the researcher's expectancy). The probability of this error is often called a test size and usually denoted as α (Alpha); a threshold value defined by the researcher to fix the probability of a Type I Error is said to be Significance Level. Traditionally, one rejects the null hypothesis if the p-value is less than or equal to the significance level, usually α = 0.05 or α = 0.01, corresponding respectively to a 5% or 1% chance of rejecting the null hypothesis when it is true (Type I Error) and the result of Hypothesis Testing sounds like "we accept (reject) the null hypothesis at the 5% level".

Note
Instead of comparing p-value with significance level null hypothesis test can be performed by calculating the data-based test statistics. We fail to reject null hypothesis if test statistics is between left and right borders of the interval which is called the region of acceptance.

The Type II Error (or false negative) is the decision to accept the null hypothesis when it is in fact false as the yellow area on the diagram presents. The probability of such error is usually denoted as β (Beta) and is related to what is known as Statistical Power which measures the ability of a statistical test to verify the falsity of the null hypothesis. Statistical Power is expressed as 1-β, where β is the probability of a Type II Error. In general, the specific value of is unknown being affected by many aspects of the experiment as well as by the statistical procedures chosen by the researcher.

Obviously, having a significant and powerful experiment is desirable but in practice there is often a trade-off between the two error types. Based on the application of the error, one type may be more serious than the other. Typically, false positives are particularly undesirable in real world applications as they result in much wasted efforts, so the prevailing standpoint is that Significance Level is a top priority yet keeping Statistical Power adequate (power of 0.8 is considered as enough to detect a reasonable departure from the null hypothesis). Experiments with small sample sizes can frequently be underpowered to provide acceptable Hypothesis Testing quality and the only way to minimize both error types is to possibly increase the sample size if it is feasible.

In economic theory and econometric, stationarity is of particular interest being one of conceptual basics and used while making practical decisions.

General definition of stationary stochastic process requires unchanged joint probability distribution of the process' realizations (data series) when they shifted in time or space. In practice, a weaker form of stationarity (known as a weak-sense stationarity, WSS) is often employed which requires just two distribution parameters unchanged over time/space, namely, the mean and the variance.

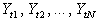
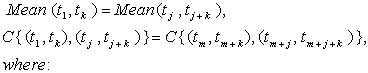
Given time series observations of a process at time points t_i , WSS conditions are:

• denotes a subset (sample) of the size k;

• j and m denote shifts (starting time points) of samples;

• C is the autocovariance which depends only on the shift between the samples.

Constructing a test statistic, i.e. a parameter that can adequately measure stationarity of time series data, is a necessary step. For this, a commonly used approach is to describe a data series with the first order (or higher) autoregressive model:

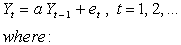
• Y₀ = 0 ,

• a is a real number,

• e is zero-mean normally distributed variable,

The notable fact about this model is that it generates:

• (convergent) stationary time series, if |a| < 1,

• non-stationary random walk time series with the variance diverging to infinity with respect to t, if |a| = 1,

• non-stationary time series with exponentially growing variance, if |a| > 1.

The random walk case, a unit root process (|a| = 1 ), corresponding to a process of taking successive random steps, is of special emphasis in economics and econometric. In economical theory, the efficient-market hypothesis states that stock market prices evolve according to a random walk and is used to model shares prices and other factors.

One can convert a random walk process to a stationary equivalent as the first difference of the unit root process will be stationary:

Note
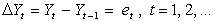
Statistical hypotheses about stationarity based on process root analysis are adequate to the extent of validity of the autoregressive model used.

Stationarity is also used as a tool for de-trending of time series data – detecting and removing long-term trends to emphasize short-term changes.

A process is described as trend stationary (or stationary around a trend) if it is a linear combination of a stationary process and one or more processes exhibiting a trend, so that if after trends were removed it would be stationary.

Two abstract classes inherit from HypothesisTest: OneSampleTest and TwoSampleTest. First class represents base one-sample statistical hypothesis test, and the second class represents two-sample test.

The following enumerators are in the base HypothesisTest class:

The HypothesisTest class has following implemented properties:

OneSampleTest supports update methods for the following sample representation:

TwoSampleTest supports update methods for the following sample representation:

Note
Update methods do not affect the samples. In all tests if update method takes parameters (such as mean, variance, edges, etc.) they are saved for future updates by update methods without these parameters. With one exception: in Wald-Wolfowitz test update without boundary updates boundary to mean value of the sample.

Reference