Click or drag to resize

One Sample T-Test

The Student's T-Test is a one-sample t-test of the null hypothesis that data in the sample are a random sample from a normal distribution with specified supposed mean and unknown variance, against the alternative that the mean is different.

This topic contains the following sections:

T-Test Specification

For one sample T-test we consider the time series HT Time Series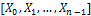

In testing the null hypothesis that the population mean is equal to a specified value μ0, one uses the statistic

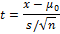
HT TTest Stat

where 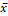HT Sample Mean is the sample mean, s is the sample standard deviation of the sample and n is the sample size. The degrees of freedom used in this test is n − 1.

Default supposed mean value is 0.

Under the null hypothesis the test statistic either exactly follows or closely approximates a t-distribution. Once a t-value is determined, a p-value can be found using values from Student's t-distribution (see the property in implementation section). If the calculated p-value is below the threshold chosen for statistical significance (usually the 0.10, the 0.05, or 0.01 level), then the null hypothesis is rejected in favor of the alternative hypothesis.

This statistics can be used to carry out either a one-tailed test or a two-tailed test.

Implementation

The following constructors create an instance of TTest class.

Constructor

Description

Performance

two-tailed T-test, default significance level

Constructor without parameters. Creates TTest instance with default significance level for two-tailed test.

methodTTest

default significance level

Creates TTest instance with default significance level and user defined tail.

methodTTest(Tail)

two-tailed test, user defined significance level

Creates TTest instance for two-tailed test and user-defined significance level.

methodTTest(Double)

user defined tail and significance level

Creates TTest instance with user defined significance level and tail.

methodTTest(Double, Tail)

The class provides the following methods:

Method

Description

Performance

update

Updates test statistic using provided sample and supposition about mean value.

Double array series:

methodUpdate(Double, Double)

Vector series:

methodUpdate(Vector, Double)

The class provides the following properties:

Property

Description

Performance

region of acceptance

We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance.

Region of acceptance left border:

PropertyAcceptanceRegionLeft

Region of acceptance right border:

PropertyAcceptanceRegionRight

p-value

The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true.

PropertyPValue

Code Sample

The example of TTest class usage:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class TTestSample
 9    {
10        static void Main()
11        {
12            // Create an instance of normal distribution.
13            Normal distr = new Normal(3, 1);
14
15            // Generate random sample from normal distribution.
16            Vector series = distr.Sample(100);
17
18            // Create an instance of TTest.
19            TTest test = new TTest(0.05, Tail.Both);
20            test.Update(series, 0);
21
22            Console.WriteLine("Test Result:");
23            // Test decision
24            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
25            // The statistic of TTest test.
26            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
27            // The p-value of the test statistic.
28            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
29
30        }
31    }
32}

See Also